![[LinuxFocus-icon]](../../common/images/logolftop_319x45.gif) |
LinuxFocus article number 243
http://linuxfocus.org
|
|
|
|
|

por Pierre Loidreau
<pierre.loidreau/at/ensta.fr>
Sobre o autor:
O Pierre trabalha como professor-Investigador na ENSTA (Escola
Nacional Superior de Técnicas Avançadas). O seu campo de investigação
diz respeito a "sistemas encriptados" baseados na teoria de correcção
de erros. "Joga" com o linux todos os dias... e ténis muito
frequentemente.
Traduzido para Português por:
Bruno Sousa <bruno/at/linuxfocus.org>
|
Introdução à criptografia

Abstrato:
Este artigo foi publicado primeiro numa revista de Linux Francesa,
numa edição especial focando a segurança. O editor, os autores, os
tradutores, gentilmente, permitiram a LinuxFocus de publicar cada
artigo desta edição especial. De acordo, a LinuxFocus apresentar-lhos-à
mal estejam traduzidos para Inglês. Obrigado a todas as pessoas
envolvidas neste trabalho. Este genérico será reproduzido para cada
artigo tendo a mesma origem.
_________________ _________________ _________________
|
O porquê da criptografia - 2500 anos de história.
A origem da criptografia, provavelmente, remonta ao princípios da
existência humana, logo que as pessoas tenham tentado aprender a
comunicar. Consequentemente, tiveram de encontrar meios para garantir a
confidencialidade de parte das suas comunicações. Contudo o primeiro
uso deliberado de métodos técnicos para encriptar mensagens pode ser
atríbuido aos antigos Gregos, em meados do século VI A.C. uma vara,
chamada "scytale" foi utilizada. O emissor enrolaria uma pedaço de
papel à volta da vara e escreveria a sua mensagem longitudinalmente
nela. Depois abria o papel e enviáva-o para o endereço respectivo. A
desencriptação da mensagem sem o conhecimento do comprimento das varas
- actuando aqui como uma chave secreta - era considerado impossível.
Mais tarde os romanos utilizaram o código cifrado de César para
comunicar (uma terceira letra do alfabeto).
Os próximos 19 séculos foram devotados à criação de técnicas de
encriptação experimentais, inteligentes, em que, cuja segurança,
actualmente, reside no quanto o utilizador confia nelas. Durante o
século XIX, o Kerchoffs escreveu os princípios da encriptação moderna.
Um destes princípios afirmava que a segurança de um sistema encriptado
não residia no processo de encriptação em si, mas sim na chave que era
utilizada.
Assim, deste ponto de vista, era esperado que os sistemas de
encriptação seguissem estes requisitos. Contudo, os sistemas
existentes, ainda carecem de cálculos matemáticos e por conseguinte,
de utilitários para medir o benchmark de resistência a ataques. Melhor
seria se alguém atingisse o objectivo mor da criptografia e encontrasse
um sistema, incondicionalmente, 100% seguro ! Em 1948 e 1948, foram
adicionadas bases científicas à criptografia com 2 papeis de Claude
Shannon: "Uma Teoria Matemática da Comunicação" e, principalmente, "A
Teoria de Comunicação de Sistemas Secretos". Estes artigos afastaram
esperanças e preconceitos. O Shannon provou a cifração de Vernam que
havia sido proposta alguns anos antes - e também a renomeou para One
Time Pad -- era o único sistema, incondicionalmente, seguro que alguma
podia existir. Infelizmente, tal sistema não era possível pô-lo em
prática... Esta é a razão porque, nos nossos dias, a evolução dos
sistemas de segurança é baseada em segurança computacional. Um defende
que a chave de cifração é segura se nenhum ataque conhecido não faça
mais do que procurar por todas as chaves possíveis.
AES (Padrão avançado de Encriptação)
Recentemente, em Outubro de 2000, o NIST (National Institute of
Standards and Technology) anunciou um novo padrão de uma chave secreta
de cifragem, escolhido de 15 candidatos. Este novo padrão pretendia
substituir o velho algoritmo DES, cujo tamanho das chaves se está a
tornar muito pequeno. O Rijndael - um nome comprimido, originário dos
seus inventores Rijmen e Daemen - foi escolhido para se tornar o futuro
AES.
Este sistema de encriptação é dito ser um "bloco" de cifragem à medida
que as mensagens são encriptadas em blocos inteiros, com unidades de
128-bits. Existem múltiplas ideias que propõem a utilização de chaves
com 128, 192, 256 bits. Só para sua informação, o DES encripta blocos
de 64 bits com uma chave de 56 bits. O DES triplo, normalmente,
encripta blocos de 64 bits com uma chave de 112 bits.
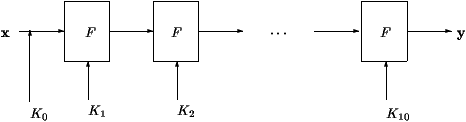
Tabela 1: Iteracções do AES
O modo operacional do AES está descrito na figura 1. Primeiro uma
chave secreta K0 é ajustada bit a bit à mensagem. Depois,
semelhantemente a todos os blocos de cifragem. A função F é iterada,
utilizando sub-chaves geradas a partir de uma rotina de expansão,
inicializada pela chave mãe.
Para o AES, a função F é iterada 10 vezes.
- A figura 2 descreve o modo como a função F é iterada para a
encriptação. Recebe um bloco de 128-bits reparticionados em 16
octetos. Primeiro a substituião S é aplicada a cada byte (octeto).
De seguida a permutação P é aplicada aos 16 octetos. A sub-chave de
128-bit, gerada pela rotina de expansão, é adicionada bit a bit ao
resultado anterior.
- A chave Ki do ciclo n°i é obtida da chave da rotina de
expansão utilizando a sub-chave K(i-1) do ciclo n°i-1 sendo K0 a
chave secreta. A rotina de expansão da chave está descrita na figura
3. Os 16 bytes da chave K(i-1) são processadas 4 a 4.
Os últimos 4 bytes são permutados utilizando a substituição S - a
mesma substituição que é utilizada na função iterada F para
substituir os bits de cada octeto. Depois os primeiros 4 bytes
resultantes são adicionados ao elemento alpha i. Este elemento é o
byte de pré-definição que depende do iterador do ciclo. Finalmente,
para obter o Ki, os 4 bytes resultantes são adicionados bit a bit aos
primeiros 4 bytes do K(i-1). De seguida o resultado é adicionado aos
próximos quatro bytes, etc.
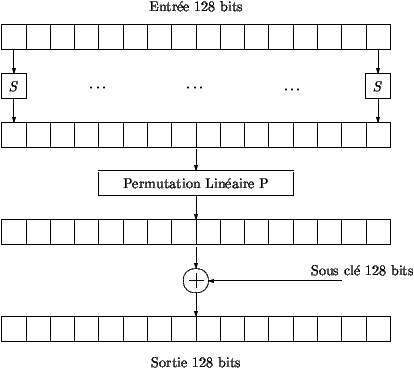
Tabela 2: Função F F
Vejemos, agora, muito resumidamente, como as substituições são
construídas e ao que corresponde a constante ai.
Tecnimente - e por razões de simplificação - um octeto deve ser
considerado como um elemento conjunto de 256 elementos, chamado um
campo finito e no qual todas as operações simples (como a adição,
multiplicação, e inverso) existem.
De facto a prévia substituição S é o inverso de tal campo. A
substituição S é especificada como sendo uma operação simples e pode,
facilmente, ser implementada.
O elemento ai corresponde
à elevação da potência i de um elemento do campo. Tais considerações
tornam as implementações do AES muito eficientes.
Como o AES é somente construído através de operações de bitwise, isto
dá-lhe duas grandes vantagens:
- mesmo puras implementações em software do AES são bastante
rápidas. Por exemplo uma implementação em C++ num Pentium a 200 Mhz
oferece uma performance de 70Mbits/s de encriptação ;
- a resistência do AES a uma análise de encriptação diferencial e
linear não depende da escolha da S-Box, como para o DES tais S-Boxes
eram suspeitas de conter uma backdoor para o NSA. De facto, todas as
operações são simples.
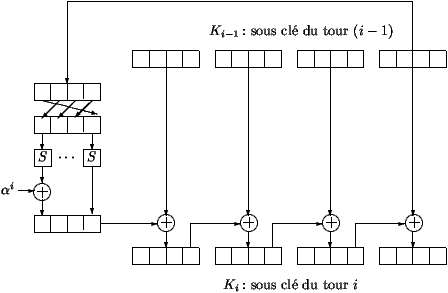
Tabela 3: Rotina da Chave de expansão
Chave Pública de encriptação
Em 1976, o Diffie e o Hellman publicaram um artigo "New Directions in
Cryptography" o qual era um objectivo real para a comunidade dos
criptógrafos. Este artigo introduzia o conceito de chave pública de
encriptação. Naquela altura, a única familia de algoritmos conhecida -
algoritmos de chaves secretas simétricas - não podia mais satisfazer as
novas necessidades que apareciam devido à explosão dos métodos de
comunicação como as redes.
Basicamente, o princípio da sua nova ideia foi a introdução do
conceito de funções de um só sentido trapdoor. Tais funções operam
facilmente num sentido mas computacionalmente impossível de inverter
sem o conhecimento de um segredo chamado trap - mesmo que a função seja
conhecida por todos. Então, a chave pública actua como função enquanto
que o trap (somente conhecido por um número limitado de utilizadores) é
chamada chave privada. Isto deu origem ao nascimento ao mundo da Alice,
Bob (e outros). A Alice e o Bob são duas pessoas que tentam comunicar
com requisitos de integridade, evitando intrusos que podem tentar
escutar ou até mesmo alterar a comuncação.
Claro que, para decrifrar a mensagem , o recipiente só precisa de
inverter a função utilizando o segredo denominado trap.
O exemplo mais simpático do criptografismo público (e, sem dúvida o
mais simples) foi apresentado dois anos mais tarde em 1978. Foi
inventado por Rivest, Shamir e Adleman e por aqui surgiu o RSA. É
baseado na dificuldade matemática da factorização inteira. A chave
privada é feita do tripleto (p,q,d) com p e q dois primos (tendo
aproximadamente o mesmo tamanho), e d é um primo relativo de
p-1 e q-1. A chave pública é formada pelo par (n,e), com
n=pq, e e o inverso do módulo de d (p-1)(q-1), por exemplo
ed = 1 mod(p-1)(q-1).
Suponha que a Alice quer enviar algum texto, encriptada com a chave
pública do Bob(n,e). Primeiro, transforma a mensagem num inteiro m
menos o n. Depois, processa
c = me mod
n,
e envia o resultado c para o Bob. Do seu lado, o Bob, cuja chave
privada é (p,q,d), processa :
cd mod n =
med mod n =
m.
Para o RSA, a função armadilha de um só sentido é a função que associa
um inteiro x <n ao valor xe mod n.
Desde o RSA, muitos outros sistemas chave de encriptação públicos foram
inventados. Presentemente uma das alternativas mais famoasas ao RSA é
um sistema de encriptação baseado em logatimos discretos.
Utilização Moderna da Criptografia
Actualmente a chave pública de criptografia é realmente interessante
porque é fácil de utilizar e resolve muitos problemas de segurança até
então sem resolução. Mais precisamente, resolve alguns problemas de
autenticação:
- Identificando Individuos: a utilização das comunicações
anónimas hoje tem o seguinte significado, a Alice quer ter a certeza
que a pessoa com quem está a falar não está a enganar ou a persuadir
o Bob. Para tal fazer, ela utiliza um protocolo de identificação.
Existem múltiplos protocolos que, no geral, assentam nos princípios
da RSA ou do algoritmo discreto.
- Autenticação de Documentos: uma autoridade autentica um
documento através de uma assinatura digital. A assinatura consiste
em adicionar alguns bits resultantes de algum processamento do
documento e da autoridade como entrada e, geralmente encontram-se na
forma de hash, através de um algoritmo de hash como o MD5 ou o SHA.
Assim, qualquer pessoa com acesso ao documento devia ser capaz de
verificar que assinatura foi atribuida pela autoridade. Para tal,
esquemas de assinatura, são utilizados. Um dos mais famosos esquemas
de assinaturas é o ElGamal - mais uma vez baseado nos problemas de
logaritmos discretos.
Para além da chave secreta de encriptação, a chave-pública de
encriptação fornece encriptação à base de sistemas de criptação,
garantindo confidencialidade nas comunicações.
Imaginemos que a Alice quer comunicar secretamente com o Bob. A Alice
obtem a chave pública do Bob num directório público e, encripta a sua
mensagem com esta chave. Quando o Bob recebe o texto encriptado, ele
usa a chave privada para decifrar o texto encriptado e lê o texto
inicialmente limpo. Ambas as chaves têm regras diferentes, isto explica
por que tais sistemas são designados de sistemas de encriptação
assimétricos - referindo os sistemas com chave de encriptação para
cifrar e decifrar são conhecidos como sistema de encriptação
simétricos.
A chave pública de encriptação oferece um outro grande benefício em
relação à chave secreta de encriptação. De facto, se n utilizadores
comunicarem através de uma chave encriptada secreta, cada um deles
precisa de uma chave diferente para cada pessoa no grupo. Assim, têm de
ser arranjadas n(n-1) chaves. Se o n representa milhares de
utilizadores então milhões de chaves precisam de ser arranjadas... Para
além disto, adicionar um utilizador ao grupo não é tarefa fácil, porque
novas n chaves precisam de ser geradas para o utilizador poder
comunicar com todos os membros do grupo. Depois, estas novas chaves
precisam de ser enviadas de volta para o grupo. De modo contrário, nos
sistemas de encriptação assimétricos, as n chaves públicas dos membros
são arquivadas num directório público. Adicionar um novo utilizador,
consiste, simplesmente, em adicionar a sua chave pública ao directório.
Usar uma chave pública ou privada: encontrando a melhor combinação
O parágrafo anterior explicou que a chave pública de encriptação
resolveu muitos problemas com os quais a chave privada não conseguia
lidar. Pode questionar-se porque é que foi desenhado o AES.
Actualmente, existem duas grandes explicações para esta escolha.
- Primeiro, uma razão prática. Geralmente, os sistemas de
encriptação com chave pública são muito lentos. Por exemplo, as
implementações de software do RSA são mil vezes mais lentas que o
AES, e o RSA não foi desenhado tendo em mente a implementação de
hardware. A transmissão de informação é tão crucial nos dias de hoje
que não podemos estar limitados por um algoritmo secreto.
- Segundo, o núcleo da estrutura dos sistemas de encriptação
com chave pública conduz a outros problemas de segurança.
Por exemplo, os sistemas de encriptação com uma chave pública
requerem tamanhos de chaves maiores - para um nível de segurança
correcto - que os sistemas de encriptação com chave secreta.
Actualmente a ideia e importância do tamanho da chave dos sistemas
de encriptação só deve ser considerada nos sistemas de encriptação
com chave secreta. De facto, tais sistemas assentam no facto que só
ataques de força-bruta é que os pode derrotar, ou seja enumerando
todas as possibilidades para as chaves. Se o tamanho da chave for de
128 bits então devem ser enumeradas 2128
possibilidades.
Mas com os sistemas de encriptação de chave pública, o tamanho da
chave só é interessante quando se considera o mesmo sistema. Por
exemplo, o RSA com uma chave de 512 bit é menos seguro que o AES
com uma chave de 128 bit. O único modo correcto de avaliar um sistema
de encriptação de chave pública é estimar a complexidade do ataque
mais bem conhecido e, isto é ligeiramente diferente: um nunca sabe se
uma nova invenção vai comprometer a segurança do sistema.
Recentemente, um grupo de pesquisadores, facturizou, com sucesso, um
inteiro de 512 bit. Consequentemente, para um nível correcto de
segurança, o conselho normal é utilizar números de 1024 bits.
Por conseguinte, para pura encriptação, os algoritmos de chave secreta
são preferidos- quando é possível utilizá-los. Zimmermann trabalhou sob
uma solução híbrida interessante, implementada no PGP. Basicamente
quando a Alice e o Bob querem comunicar com factores de integridade
utilizando o algoritmo de chave secreta (o PGP usa o IDEA):
- A Alice e o Bob negoceiam uma chave utilizando um protocolo
de troca de chaves. Os protocolos de troca de chaves utilizam chaves
de encriptação pública. Um dos mais famosos protocolos assenta no
algoritmo de Diffie-Hellman's.
- Depois, comunicam utilizando o algoritmo IDEA.
Quando a comunicação termina, a chave de negociação da sessão é
descartada. Tais sistemas usam ambas as chaves secretas e públicas dos
sistemas de encriptação. Normalmente, as pessoas consideram como sendo
a parte mais insegura o protocolo de troca das chaves.
Bibliografia
História da Criptografia:
- S. Singh : Histoire des codes secrets. Jean-Claude
Lattès, 1999.
- D. Kahn : The Codebreakers: the story of secret
writing. MacMillan publishing, 1996.
Para o AES :
Criptografia em geral:
2005-01-14, generated by lfparser_pdf version 2.51




