LinuxFocus article number 345 http://linuxfocus.org

par Ralf Wieland <rwielandQzalf.de> L´auteur: Je travaille sur les simulations d'environnement, les réseaux neuraux et les systèmes flous en les programmant. Ces derniers sont réalisés sous Linux (depuis le 0.99pl12). De plus, l'électronique et le matériel m'intéressent dans la mesure où je peux les relier à Linux. Traduit en Français par: Iznogood <iznogoodQiznogood-factory.org>

Linux pour la Science - Ou comment un outil utile pour les réseaux neuraux a été développé Résumé: Cet article démontre l'adéquation de Linux pour les logiciels scientifiques. Un intérêt particulier sera porté sur le développement d'outils scientifiques pour la simulation de paysages. Comme exemple, nous introduirons un simulateur de réseau neural, qui a été placé sous GPL. _________________ _________________ _________________

Quel est le but?

Je travaille dans un institut de recherche qui est engagé dans la recherche sur les paysages. Des questions comme celles qui suivent sont approfondies:

• Pourrons-nous encore boire l'eau pendant 50 ans sans restrictions ?
• Quels plantes et animaux survivront si le climat change; y aura-t-il encore des forêts et les terres seront-elles encore arables ?
• Où se dépose la poussière du désert et comment s'étend le désert ?

Détail du travail au jour le jour avec Linux

Le travail quotidien de relevé d'informations, consistant en l'analyse de données, la récrimination envers les mesures de données incomplètes, le reformatage en différents formats, l'écriture de rapports, etc., bénéficie énormément à Linux. Même si quelques-uns pensent que Excel et les autres peuvent tout faire, la combinaison de Perl, Emacs, octave [www.octave.org], R [www.r-project.org] etc. démontre leur capacité dans la bataille avec les données. Perl est très polyvalent, pas seulement pour la conversion de données; il recherche dans la base de données (MySQL), exécute des calculs, etc., rapidement et d'une manière reproductible. Ce dernier point est particulièrement important car le travail manuel mène fréquement à des erreurs dans les données, ce qui est rarement le cas avec l'application de scripts éprouvés. L'écriture d'articles avec LaTeX est convaincant par sa qualité de présentation. Linux fournit des outils qui le rendent intéressant pour le travail scientifique. Nous ne voulons cacher aucun désavantage: il faut être intensément impliqué dans l'utilisation de ces outils. Tout ne peut pas être réalisé intuitivement et tout le monde ne peut être une bête de programmation.

L'étape suivante - Les outils de Développement

Pourquoi doit-on tout développer seul, tout n'est-il pas disponible ? Il existe des outils très performants disponibles pour la simulation, comme Matlab [www.mathworks.com]. Pour traiter des données géographiques, le Geographic Information Systems (GIS) comme ARCGIS [www.esri.com/software/arcgis] ou le logiciel libre Grass [grass.itc.it] sont disponibles. Pour les statistiques, ce n'est pas très différent. Donc, pourquoi continuer à développer ?
Le problème n'est pas la performance des composants seuls mais leur collaboration dans un système. Dans une simulation, les sous-tâches doivent être effectuées par des programmes différents, qui ne peuvent qu'imparfaitement communiquer, ce qui signifie par des interfaces produites par les utilisateurs. Avec pour facteur aggravant que les données disponibles sont concentrées (données spatiales) avec de gros taux d'erreurs. Les simulations essentielles doivent s'accommoder de ce fait. Un algorithme doit fournir des résultats utiles même si les données entrées ne correspondent pas tout à fait, un avertissement doit être donné dans ce cas. Le traitement de données concentrées (des matrices de plus d'un million d'éléments formant la règle) nécessite des algorithmes rapides. Des algorithmes robustes et rapides ne peuvent souvent être implémentés qu'en les développant soi-même.
L'inconvénient principal des systèmes commerciaux est le secret qui entoure leur code source. Comment les scientifiques peuvent-ils développer et échanger des modèles si les sources ne sont pas ouvertes ? De ces conclusions, il a été décidé de développer un "Spatial Analysis and Modeling Tool" (SAMT ; Outil d'Analyse et de Modélisation Spatial) comme logiciel open source.
C'est un outil de simulation, incorporant la gestion de données spatiales, les interfaces à la base de données MySQL et à GIS. Il contient les fonctions fondamentales pour la gestion de données sous forme de trames, il peut les manipuler (mélange, distances, interpolation, etc.) et peut générer des présentations en deux ou trois dimensions.
Note: les données en trames sont basées sur la division de cartes en petits carrés. L'information est stockée dans plusieurs couches de données en trames. Un modèle accède à l'information des couches. En plus de l'approche de l'information en profondeur, celles environnantes du même niveau sont fondamentales. Les dernières forment la base pour la modélisation des flux de matériaux latéraux, lorsqu'ils provoquent l'érosion du sol, causé par le vent et l'eau.
SAMT génère la structure dans laquelle les outils -comme un interpréteur flou (très rapide) et l'outil de réseau neural - peuvent s'y adapter. Les modèles flous et l'outil de réseau neural (nnqt) - peuvent aussi y être adaptés. Les modèles flous servent à intégrer la connaissance de l'expertise dans la simulation. Un expert peut souvent décrire un processus ou même le contrôler, même si aucun modèle mathématique n'est disponible. Les réseau neuraux sont des processus qui nous permettent de dériver des corrélations fonctionnelles depuis la mesure des données. Ce qui suit peut introduire le développement de l'outil des réseaux neuraux.

Qu'est ce qu'est un réseau neural ?

Un réseau neural artificiel consiste en plusieurs couches. La première couche sera chargées avec les données devant être traitées, sous la forme de chiffres en virgule flottante. La couche entre l'entrée et la sortie qui n'est pas directement visible depuis l'extérieur est appelée 'couche cachée (hidden layer)'. Plusieurs couches cachées peuvent être quelquefois présentes. La couche de sortie de notre exemple ne possède qu'un élément. Ce type d'architecture est utilisé pour élaborer une fonction à plusieurs entrées et une sortie. Les couches cachées sont nécessaires pour cartographier les comportements non-linéaires, par exemple, la fonction x^2-y^2. Comment un réseau connaît-il la fonction voulue ? Bien sûr, initialement, le réseau ne connaît pas la fonction. Les connexions (valeurs statistiques) entre les éléments (noeuds) sont attribuées avec des valeurs stochastiques. Pendant le processus d'apprentissage, l'algorithme tente de changer ces valeurs de telle manière que la moyenne de l'erreur au carré entre les sorties calculées et prédéterminées soit la plus petite possible. Il existe de nombreux algorithmes pour le faire, nous n'allons pas nous étendre dessus ici. Trois algorithmes ont été implémentés dans nnqt. Avec une entrée aléatoire pour une sortie désignée, le processus est appelé 'supervised learning (apprentissage supervisé)'.

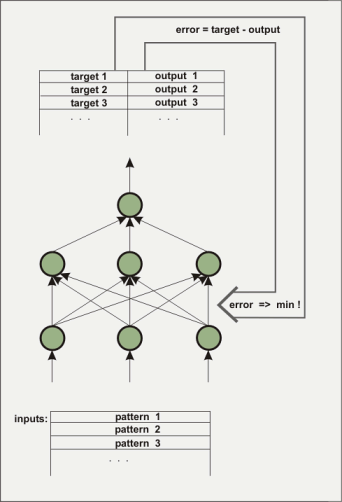
Le réseau est formé pour détecter s'il a atteint une erreur suffisamment basse par rapport aux données de contrôle (il est sage de séparer une partie des données avant l'apprentissage pour les utiliser comme données de contrôle et vérifier l'accomplissement de l'apprentissage). Les valeurs statistiques déterminent le comportement du réseau et elles sont stockées dans ce but. Qu'est-il possible de faire avec un tel réseau? En plus des applications telles que les outils de modélisation en science, il existe beaucoup d'applications plus ou moins sérieuses. Il existe des tentatives pour prédire les cours de la bourse. Je n'ai pas eu de succès avec mais peut être que quelqu'un d'autre en aura.
Une autre possibilité intéressante serait d'utiliser un réseau neural pour des prévisions météo à court terme. Les données des stations de météo automatique, par exemple, pourraient être utilisées pour apprendre à un réseau neural. La pression atmosphérique et ses changements seraient utiles, de même que les précipitations. Les symboles des stations de météo suivent ces motifs. Un réseau neural pourrait peut être mieux le faire? Pour réaliser ses propres expérimentations nnqt est disponible sous GPL.

L'outil de réseau neural nnqt

Les scientifiques ont initié le développement de l'outil de réseau neural avec le souhait que je puisse analyser leurs données collectées. Ils voulaient un outil aussi simple que possible, capable d'être utilisé pour les applications spatiales, ce qui signifie : ils souhaitaient voir comment les résultats sont associés au placement spatial. Bien sûr, il existe d'excellents outils de réseaux neuraux sur le marché. Même des outils libres comme SNNS [www-ra.informatik.uni-tuebingen.de/SNNS/] ou des bibliothèques logicielles comme fann [fann.sourceforge.net] sont disponibles. SNNS est puissant mais il n'est pas aussi facile à utiliser pour quelqu'un qui ne programme pas, sa sortie est en C. Dans cette optique, il peut être déconcertant pour l'utilisateur occasionnel. nnqt doit satisfaire un nombre d'exigences :

• Intégration dans SAMT (utilisation de trames de données comme jeux d'apprentissage), utilisation des réseaux stockés dans les modèles spatiaux)
• Manipulation interactive, intégration de techniques d'analyse
• Utilisation d'un outil extérieur à SAMT

Le développement de nnqt

Le développement a été fait avec les étapes suivantes :

1. Développement et test des algorithmes
2. Implémentation comme application qt
3. Intégration dans SAMT

Développement et test de l'algorithme

Il existe beaucoup de bonne littérature sur les réseaux neuraux. Parmi les ouvrages représentatifs, ce livre peut être mentionné. Néanmoins, il y a quelquefois des lacunes qui doivent être comblées avec votre propre expérimentation ou par les échanges avec les autres. J'aime le travail rapide avec Matlab utilisant l'algorithme Levenberg-Marquardt. C'est seulement après des recherches internet intensives que j'ai trouvé une copie locale d'un article [www.eng.auburn.edu/~wilambm/pap/2001/FastConv_IJCNN01.PDF][ de 105533 octets] qui décrit l'utilisation de cet algorithme pour les réseaux neuraux. C'était basique. J'ai "seulement" eu à intégrer ma fonction tanh favorite (tangente hyperbole) dans l'algorithme. C'est aussi pour cela que j'ai utilisé le logiciel Linux : le système algébrique par ordinateur Maxima [maxima.sourceforge.net]. Il est possible, avec ce type de système, de manipuler des équations compliquées, résoudre des équations différentielles et ainsi de suite, opérations qui ne sont pas si simples à résoudre avec du papier et un crayon. Maxima a rendu possible la réalisation des manipulations nécessaires et l'implémentation de la première version de l'algorithme en C en une session de week-end. L'implémentation en C a été effectuée pour tester et pour modifier les paramètres. En utilisant le système de simulation open source desire [members.aol.com/gatmkorn] (moults remerciements au développeur, Prof. Korn!) comme outil de comparaison, le modèle initial de calcul a pu être exécuté. L'algorithme nouvellement implémenté n'a pas trop mal réussi. Le temps d'apprentissage du problème xor, un exemple de test favori pour les réseaux neuraux a été achevé en 70ms sur un ordinateur avec un Pentium à 3GHz. (La majorité de ce temps provient des opérations de lecture du disque dur, le temps sur un ordinateur avec un Athlon 750MHz était beaucoup plus important).
Comme alternative, l'algorithme bien connu "back propagation" a été implémenté et analysé. Après ces préparations, qui forment la base pour de futures améliorations des algorithmes, l'implémentation de la boîte à outil a continué.

Implémentation et résultats

Comme environnement de développement, je préfère qt, il est bien documenté et je peux utiliser l'éditeur Emacs. Le dessinateur qt assiste dans la conception des surfaces. Malgré ceci, ces options ne sont pas suffisantes pour le développement de nnqt. J'ai besoin de quelque chose comme des diagrammes, des échelles, etc.  Pour ceci, la communauté des développeurs a été d'une grande aide. Les bibliothèques de qwt [qwt.sourceforge.net] et qwt3d [qwtplot3d.sourceforge.net] peuvent être utilisées, raccourcissant spectaculairement le temps de développement. Équipé de ses sources, nnqt a été construit en deux semaines. Lorsque j'ai été suffisamment content du résultat, je me suis tourné vers les utilisateurs. Ils avaient beaucoup de requêtes! Le jeu de données doit être automatiquement divisé en jeu d'apprentissage et en jeu de test, ils voulaient être capables d'assigner des noms pour améliorer l'organisation, effectuer plus d'analyses - comme des graphes avec des courbes de paramètres, etc. Pour quelques uns, j'ai pu les intégrer immédiatement, d'autres fonctionnalités prendront un peu plus de temps. Vous avez ici quelques captures d'écrans:

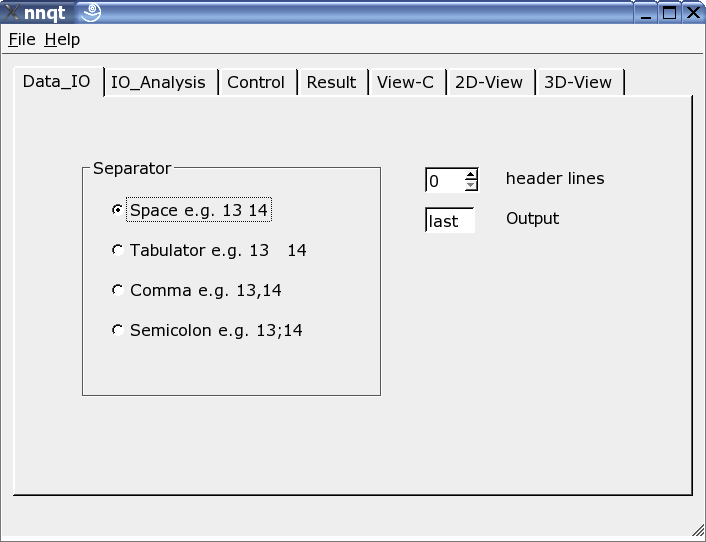
Ici, le lecteur peut être ajusté au format des données d'entrée. Divers séparateurs peuvent être utilisés, quelques lignes d'en-tête peuvent être cachées ou la cible dans le jeu de données peut être librement choisie. Note: le format de données doit être connu, comme nnqt dépend de l'entrée utilisateur.

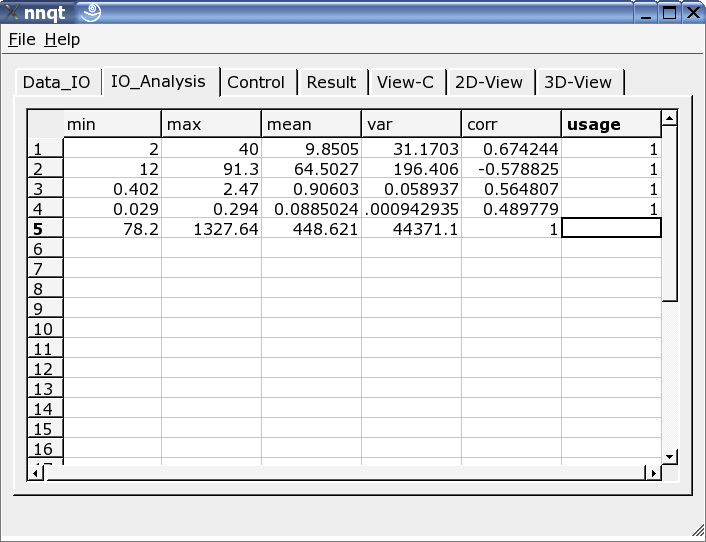
Après avoir entré les données avec succès, nous nous déplaçons directement à la page d'analyse. Nous trouvons ici quelques informations sur les données et ces dernières pour l'apprentissage doivent être sélectionnées dans toutes les colonnes. Un '1' dans la dernière marque l'entrée comme une valeur d'apprentissage. (Jusqu'à 29 valeurs d'apprentissage peuvent être utilisées.)

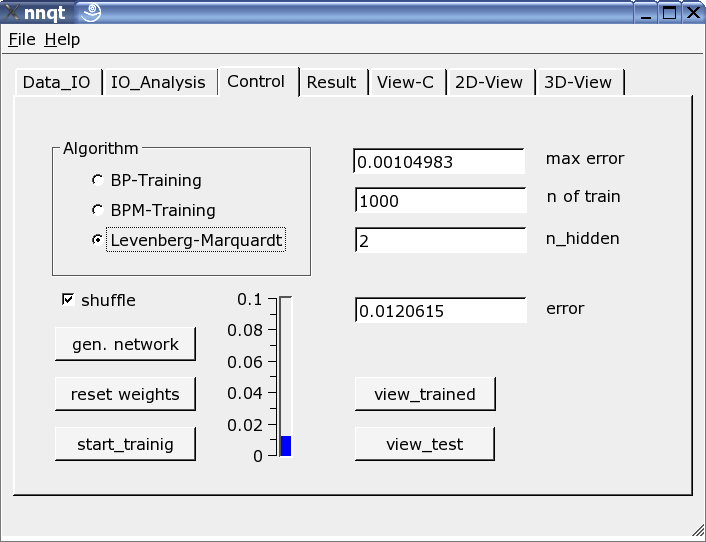
Le plus important est la page de contrôle. Le nombre d'éléments cachés, le nombre d'étapes et l'algorithme d'apprentissage sont définis ici. L'apprentissage peut être validé sur l'échelle verticale sous forme d'une barre et comme une valeur. L'apprentissage doit être répété car le paramètre de démarrage a été choisi stochastiquement et le résultat en est une fonction directe. En validant la case "shuffle", on génère une sélection aléatoire - au lieu d'une sélection séquentielle - des données d'apprentissage, ce qui est parfois avantageux. Si nous avons réussi à baisser la moyenne de l'erreur carrée suffisamment, nous pouvons obtenir le premier graphe en pressant le bouton "view_trained":

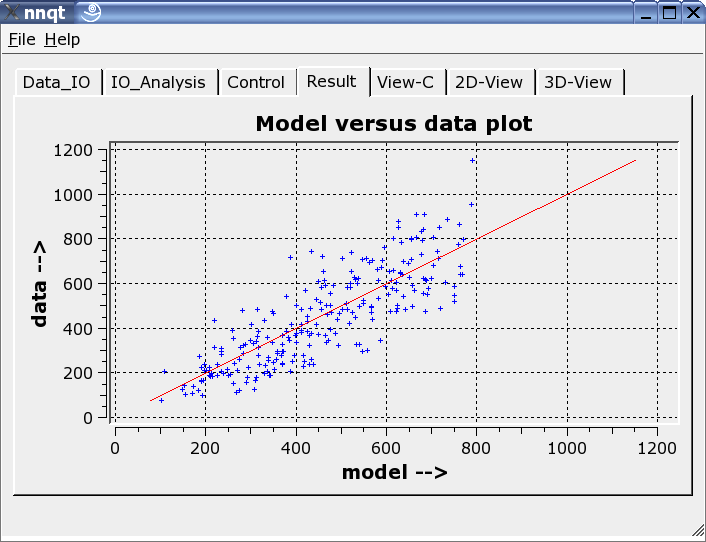
Ceci montre la comparaison entre les données d'apprentissage avec les données générés par le réseau neural. Les données doivent être idéalement sur la diagonale. Mais l'idéal ne peut être réalisé! Malgré tout, le résultat semble assez intéressant. (Les données de contrôle - ce sont celles qui n'ont pas servi pour l'apprentissage - sont marquées en rouge.) L'étape suivante permet l'analyse de la progression de la fonction. Les valeurs par défaut doivent être positionnées avec des nombres significatifs. Nous devons y faire attention car le réseau ne travaille fiablement que proche des données d'apprentissage.

Les présentations à deux ou trois dimensions peuvent être choisies.

Utilisation de nnqt

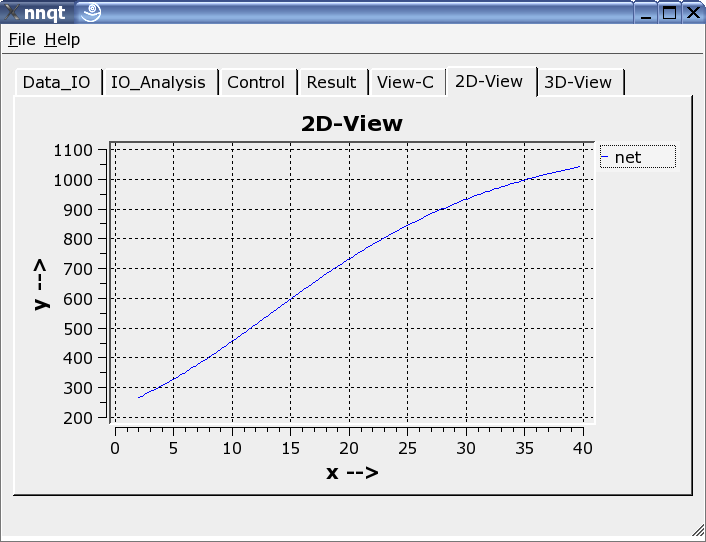
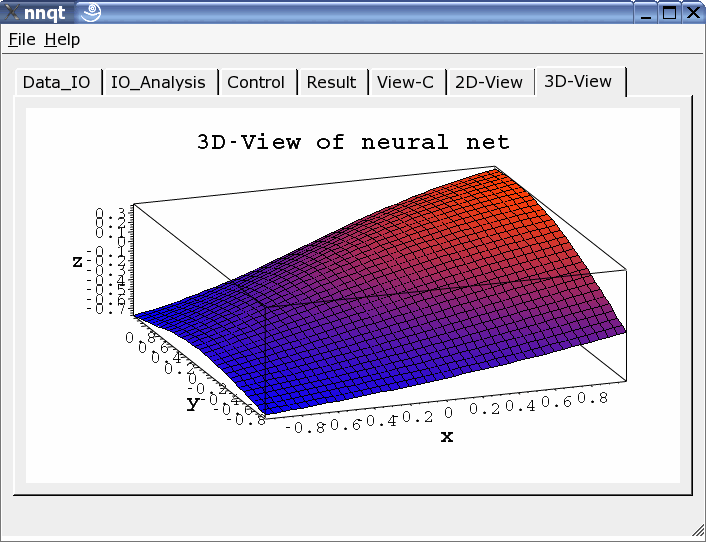
nnqt est un logiciel open source , il a été placé sous GPL. Tout le monde peut l'utiliser librement et l'améliorer. Ce dernier point étant tout particulièrement apprécié. L'installation est assez simple. Seules les bibliothèques qwt et qt doivent être installées. nnqt.tgz est simple à décompresser (tar-zxvf nnqt.tgz). Cela créera un nouveau répertoire appelé nnqt. En faisant suivre par un cd nnqt, un qmake et un make consécutivement, nous pourrons démarrer dans le répertoire nnqt . Si tout a été interprété correctement, une variable shell peut être positionnée en exécutant:
export NN_HOME=/pfad_zu_nnqt
Si nnqt est ouvert dans un nouveau terminal, les données et les modèles devraient être détectés par nnqt. J'espère que vous aurez beaucoup de plaisir avec. Pour tester le programme, un jeu de données avec deux entrées est inclus. Quelqu'un reconnaît-il la fonction qui a été apprise ? (c'est x^2-y^2 dans l'intervalle [-2..2].)

Que pouvons-nous créer avec tout ceci - je suis anxieux de voir vos idées.

Merci à la communauté

Il a été démontré que Linux est un excellent environnement de développement pour résoudre les problèmes scientifiques. J'ai pu effectuer le développement sur la base d'excellents logiciels, sans lesquels il aurait été impossible de créer un outil utilisable dans un intervalle de temps de 6 semaines. Cela fait toujours plaisir de pouvoir utiliser des logiciels libres. Pour cette raison, merci à tous les développeurs qui ont rendu ces merveilleuses choses possibles à réaliser sous Linux.

Littérature

James A. Freeman:
"Simulating Neural Networks with Mathematica", Addison-Wesley 1994

2005-01-22, generated by lfparser_pdf version 2.51