Balance del árbol
Como se mostró anteriormente, cda vez que se modifique el árbol (i.e. agreguen o eliminen elementos) corremos el riesgo de que pierda su propiedad de equilibrio en alguno de sus nodos, la cual debe conservarse si queremos obtener tiempos de ejecución de orden O(log(n)) en el peor de los casos.
La idea general que se utiliza en esta implementación de árboles AVL para implementar los algoritmos de inserción y de eliminación de nodos sobre un AVL es la siguiente:
Efectuar los algoritmos de igual forma que en los árboles binarios de búsqueda pero
en cada recursión ir actualizando las alturas y rebalanceando el árbol en caso de que sea necesario.
En the Section called Consideraciones sobre la altura de los nodos se implementó una función de tiempo de ejecución O(log(n)), peor caso, para actualizar la altura de un nodo. Así, lo que nos falta es una función que detecte un "desequilibrio" en un nodo dado del árbol y por medio de un número finito de rotaciones lo equilibre.
Important: No se demostrará aquí, pero cabe señalar la existencia de un teorema que asegura que el número máximo de rotaciones para equilibrar un árbol AVL luego de una inserción es 2 y luego de una eliminación es log(n) dónde n es el número de nodos.
En las secciones anteriores hemos ya descripto a grandes razgos cuál rotación usar en cada caso de desequilibrio. Esperamos que en el código siguiente el lector pueda formalizar tales ideas.

- Declaración de la función balancear(). Esta declaración junto con el comentario que le sigue deberían estar en un archivo de cabecera usado para la interfaz del tipo abstracto de dato árbol avl con el usuario-programador.

- Como dice en el comentario de la función, sólo se contemplarán aquellos desequilibrios cuya diferencia entre alturas es hasta 2.

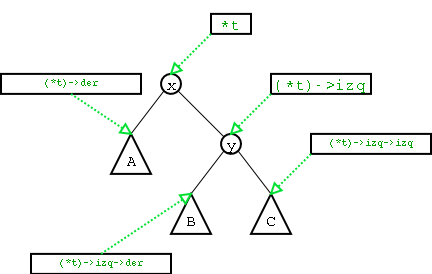
- Sabiendo que en el nodo al que apunta *t hay un desequilibrio hacia la izquierda (de diferencia de alturas 2), debemos averiguar qué clase de rotación aplicar. En Figure 12 se explica gráficamente a dónde apuntan las variables de la función en un árbol genérico.
Como puede verse en el código, nos decidimos por una rotación simple izquierda si el subárbol más pesado de (*t)->izq es el izquierdo o por una rotación doble izquierda si el subárbol más pesado de (*t)->izq es el derecho.

- Si detectamos un desequilibrio hacia la derecha, la toma de deciciones son análogas a las de un desequilibrio hacia la izquierda, las cuales ya explicamos.